Удельное тепло для идеального газа при стабильных объеме и давлении
Содержание:
Термохимия
Все химические
реакции сопровождаются тепловыми
эффектами. Более того, при некоторых
фиксированных условиях протекания эти
эффекты являются характеристическими
величинами. Так, например, как было
показано выше, при протекании изохорической
химической реакции вся подводимая и
отводимая от системы теплота ведет к
изменению внутренней энергии системы,
абсолютную величину которой оценить
нельзя, но определение ее изменения в
процессе химической реакции вполне
возможно. При протекании процессов при
постоянном давлении, подводимая к
системе или отводимая теплота равна
изменению ее энтальпии. При этом H
и U
равны только при сугубо частных условиях.
Кроме того,
абсолютные величины тепловых эффектов
химических реакций (поглощение или
отвод от системы теплоты в процессе их
протекания) являются функциями
температуры. И только в весьма узких
температурных интервалах они могут
быть приняты, в первом приближении, как
постоянные.
В связи со сказанным
необходимо стандартизовать условия
протекания химических процессов, то
есть договориться об условиях, при
которых вещества находятся в стандартном
состоянии. За стандартные приняты
следующие условия:
температура 298 К
или 25 С;
давление газа
1,035
105
Па;
жидкости в
стандартном состоянии находятся при
том же давлении (или 1 атм).
Если при протекании
реакций происходит выделение теплоты,
то изменение энтальпии (H)
отрицательно. Такие процессы называются
экзотермическими (H
А + В
С – H
В обратном случае
(поглощение теплоты) H
положительно, а реакции называются
эндотермическими (H
> 0).
А + В
С + H
Нолик, если он
приводится, в верхнем индексе H
указывает на стандартное состояние
всех участников реакции. Представленная
выше условная система получила название
термодинамической. В научной практике
все термодинамические константы в
справочниках приводятся при стандартных
условиях.
Для различных
соединений характерны свои теплоты
образования. Под теплотой (энтальпией)
образования понимают количество теплоты,
которое выделяется или поглощается при
образовании 1 моля i-того
вещества при рассматриваемых (в
справочниках – стандартных) условиях
из простых, термодинамически устойчивых
веществ.
При стандартных
условиях их принято обозначать H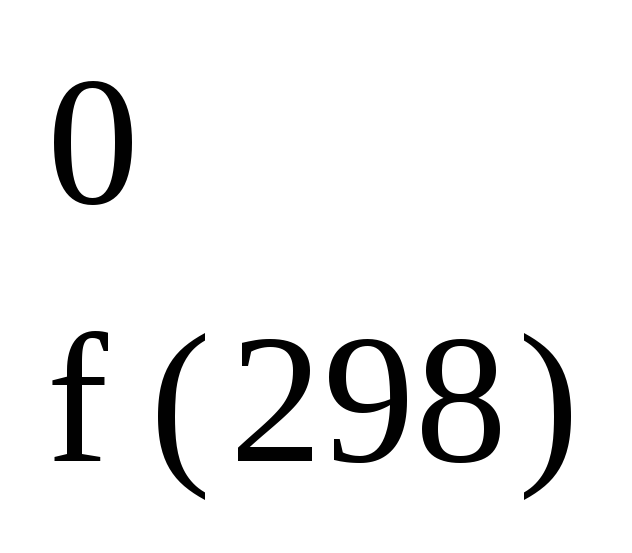
,
где f
— formation.
Для ряда процессов они приведены ниже.
С + 1/2О2
= СО; H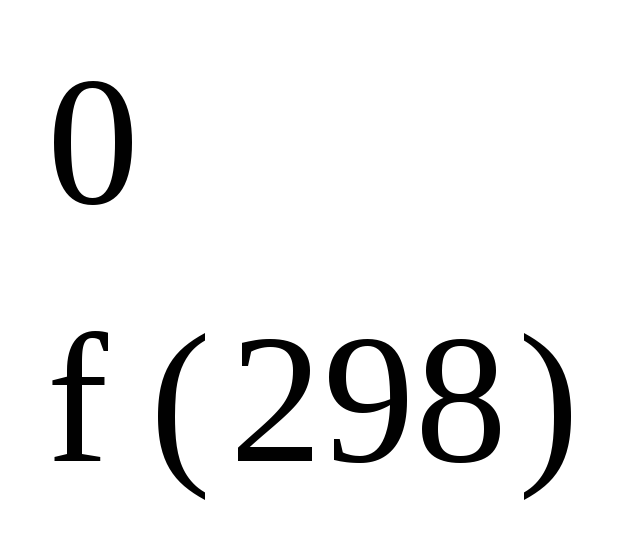
= 113,8
кДж/моль
1/2Cl2(г)
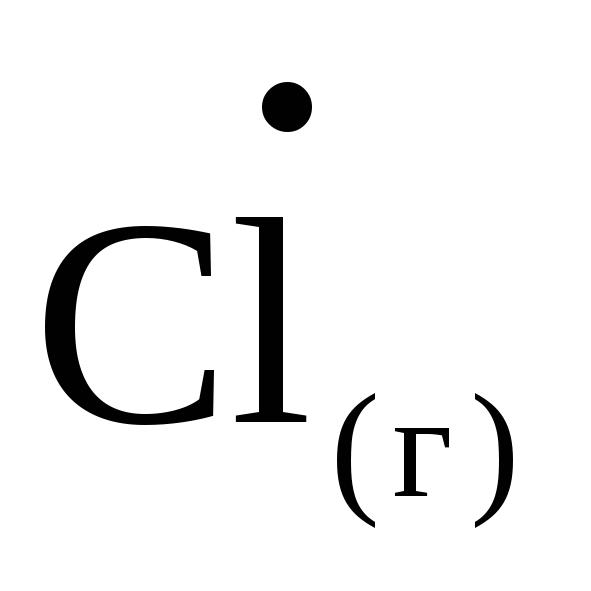; H
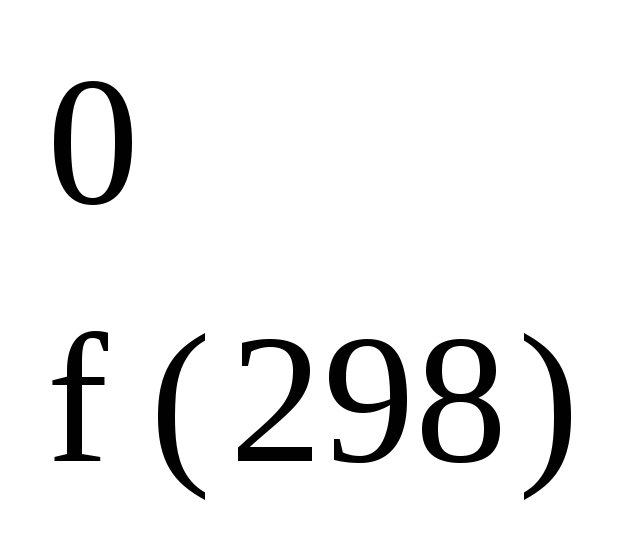
= 121,3 кДж/моль
1/2Cl2
+ е
Cl; H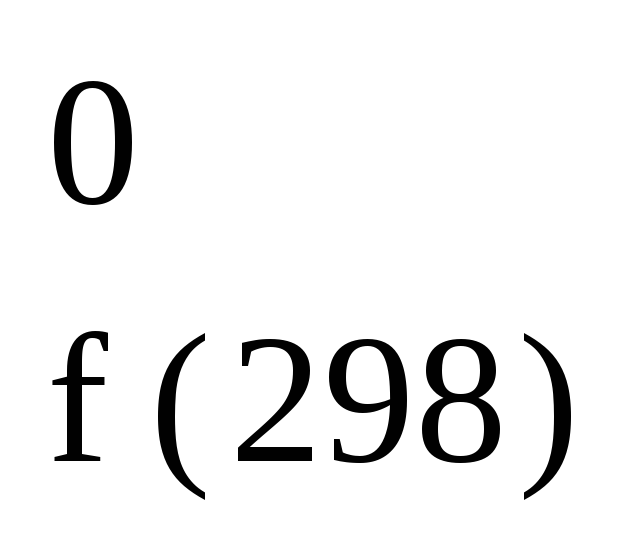
= 233,6
кДж/моль
1/2Cl2
+ е + aq
Cl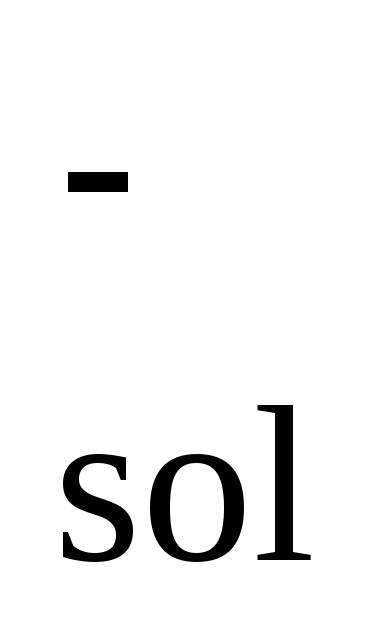
; H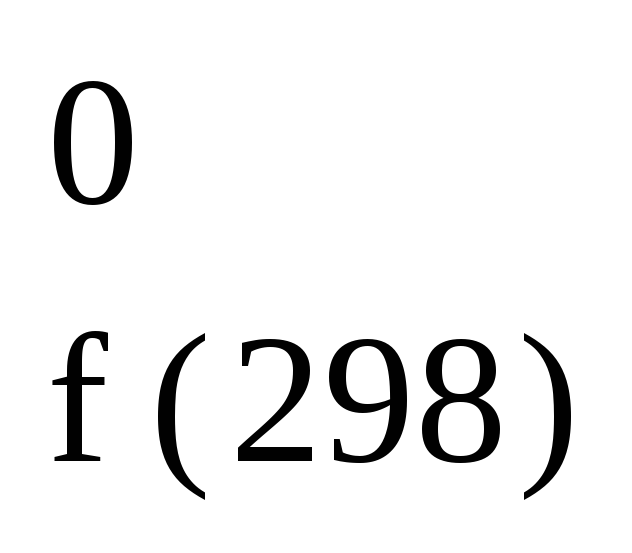
= 167,1
кДж/моль
C
+ 2H2
CH4(г);
H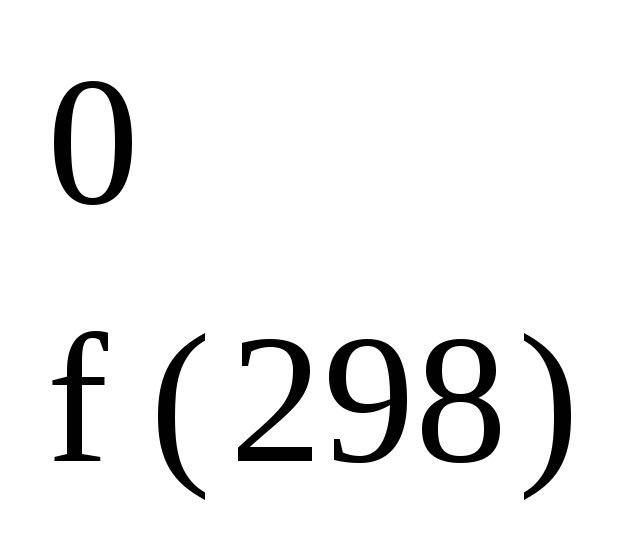
= 74,8
кДж/моль
6C
+ 3H2
C6H6(г);
H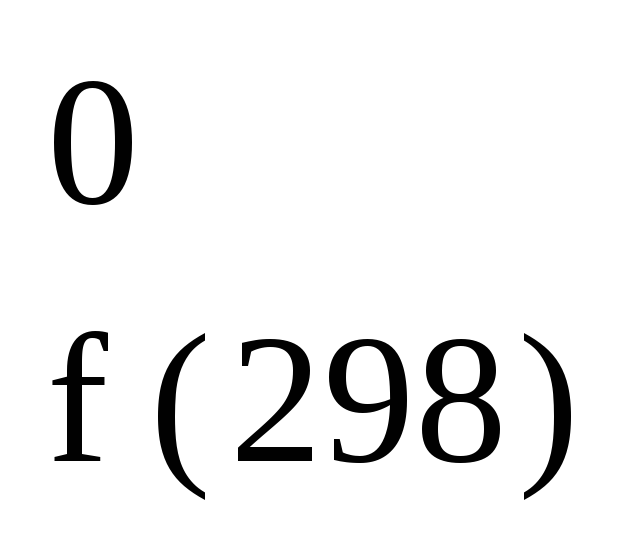
= 82,93 кДж/моль
5C
+ 6H2
C5H12(г);
(н-пентан) H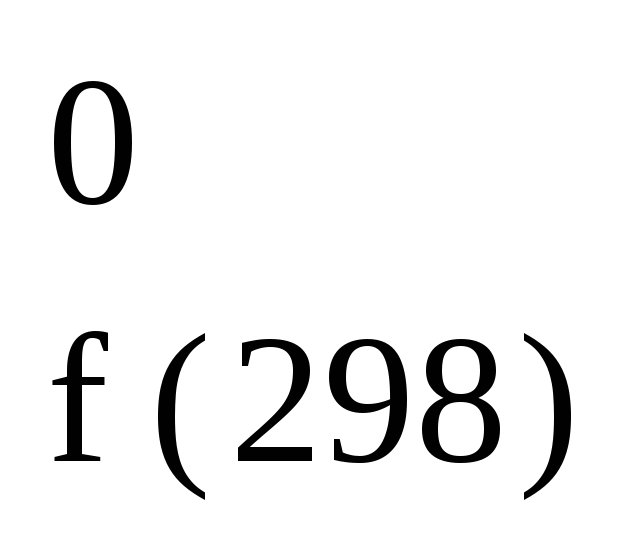
= 173,3 кДж/моль
Теплоты образования
простых веществ, термодинамически
стабильных, при стандартных условиях
приняты условно равными нулю.
Так, H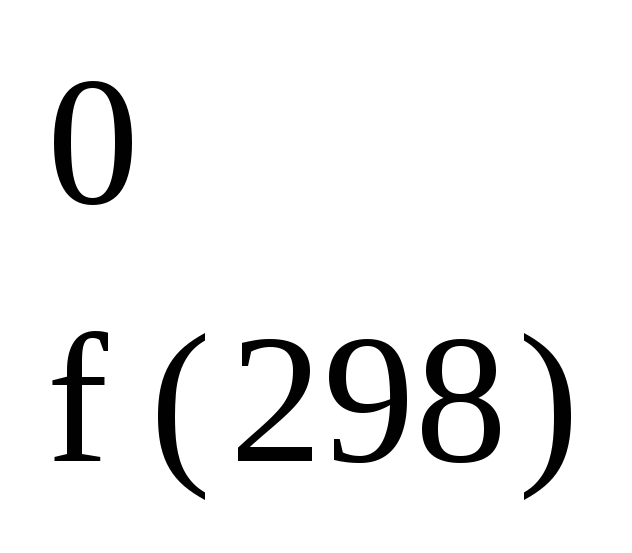
О2(г)
= 0; H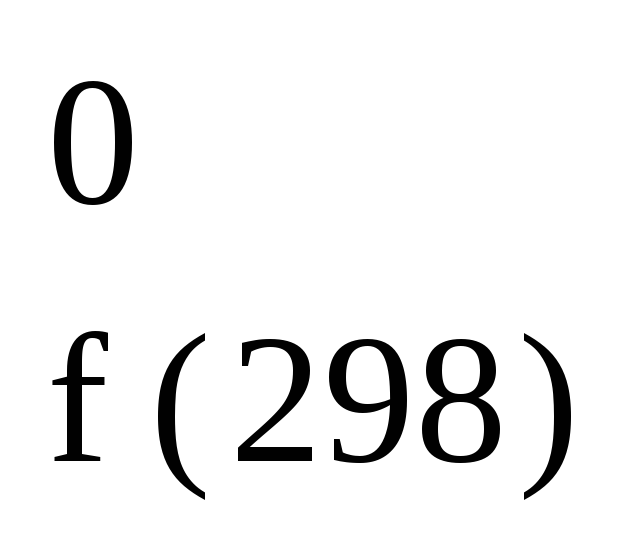
Н2(г)
= 0.
Кроме того, теплоты
образования вещества зависят от его
агрегатного состояния.
H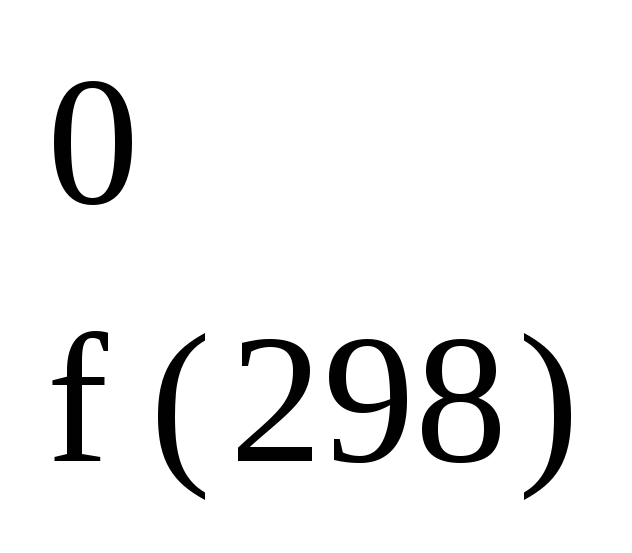
Н2О(кр)
= 291,8
кДж/моль;
H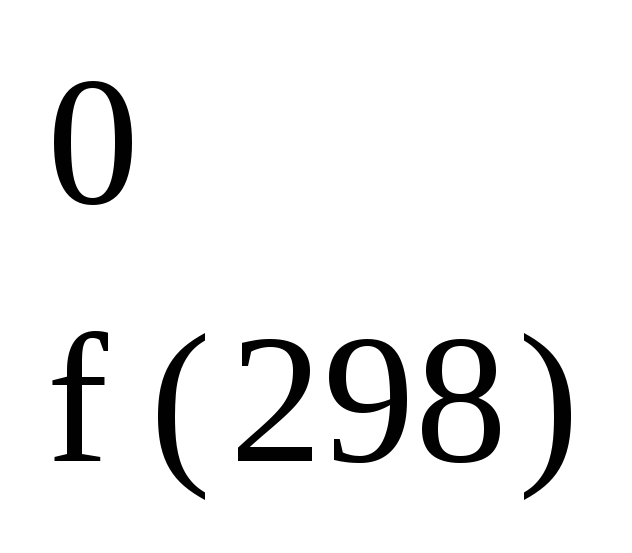
Н2О(ж)
= 285,8
кДж/моль;
H
Н2О(г)
= 187,9
кДж/моль.
В химической
термодинамике широко используется
понятие теплоты сгорания. Под теплотой
сгорания вещества понимают то количество
теплоты, которое выделяется при полном
сгорании одного моля вещества до высших
оксидов при данных условиях, учитывающих
давление и температуру. Сгорание следует
считать полным, когда C,
H,
N,
S,
Cl,
входящих в состав химических веществ,
превращаются соответственно в СО2,
Н2О(ж),
N2,
SO2
и HCl.
Под стандартной
теплотой сгорания понимают H
реакции, когда исходные вещества и
продукты сгорания до высших оксидов
находятся в стандартном состоянии.
Таким образом,
стандартные теплоты образования и
сгорания веществ, в том числе и органических
можно считать их характеристическими
константами.
Определение
Удельная теплоемкость вещества, обычно обозначаемая как c{ displaystyle c}, — теплоемкость C{ displaystyle C} образца вещества, деленного на массу M{ displaystyle M} образца:
- c=CM=1M⋅dQdТ{ displaystyle c = { frac {C} {M}} = { frac {1} {M}} cdot { frac { mathrm {d} Q} { mathrm {d} T}}}
куда dQ{ displaystyle mathrm {d} Q} представляет количество тепла, необходимое для равномерного повышения температуры образца с небольшим шагом dТ{ displaystyle mathrm {d} T}.
Как и теплоемкость объекта, удельная теплоемкость вещества может варьироваться, иногда существенно, в зависимости от начальной температуры. Т{ displaystyle T} образца и давление п{ displaystyle p} применяется к нему. Следовательно, ее следует рассматривать как функцию c(п,Т){ displaystyle c (p, T)} этих двух переменных.
Эти параметры обычно указываются при указании удельной теплоемкости вещества. Например, «Вода (жидкость): cп{ displaystyle c_ {p}} = 4185,5 Дж / К / кг (15 ° C, 101,325 кПа) » Если не указано иное, опубликованные значения удельной теплоемкости c{ displaystyle c} как правило, действительны для некоторых стандартные условия по температуре и давлению.
Однако зависимость c{ displaystyle c} на начальную температуру и давление часто можно игнорировать в практических контекстах, например при работе в узких диапазонах этих переменных. В этих контекстах обычно опускают квалификатор (п,Т){ displaystyle (p, T)}, и аппроксимирует теплоемкость константой c{ displaystyle c} подходит для этих диапазонов.
Удельная теплоемкость — это интенсивное свойство вещества, внутренняя характеристика, которая не зависит от размера или формы рассматриваемого количества. (Квалификатор «специфический» перед экстенсивным свойством часто указывает на интенсивное свойство, производное от него.)
Вариации
Введение тепловой энергии в вещество, помимо повышения его температуры, обычно вызывает увеличение его объема и / или давления, в зависимости от того, как удерживается образец. Выбор последнего влияет на измеренную удельную теплоемкость даже при том же начальном давлении. п{ displaystyle p} и начальная температура Т{ displaystyle T}. Широко используются два конкретных варианта:
- Если давление поддерживается постоянным (например, при атмосферном давлении окружающей среды), а образец расширяется, расширение вызывает работай поскольку сила давления смещает корпус или окружающую жидкость. Эта работа должна производиться за счет поставляемой тепловой энергии. Полученная таким образом удельная теплоемкость называется измеренной. при постоянном давлении (или же изобарический), и часто обозначается cп{ displaystyle c_ {p}}, cп{ displaystyle c _ { mathrm {p}}}, так далее.
- С другой стороны, если расширение предотвращается — например, за счет достаточно жесткого корпуса или увеличения внешнего давления, чтобы противодействовать внутреннему, — работа не создается, и тепловая энергия, которая пошла бы в него, должна вместо этого способствовать внутренняя энергия образца, в том числе повышение его температуры на дополнительную величину. Полученная таким образом удельная теплоемкость называется измеренной. при постоянной громкости (или же изохорный) и обозначили cV{ displaystyle c_ {V}}, cv{ displaystyle c_ {v}} cv{ displaystyle c _ { mathrm {v}}}, так далее.
Значение cV{ displaystyle c_ {V}} обычно меньше, чем значение cп{ displaystyle c_ {p}}. Эта разница особенно заметна для газов, где значения при постоянном давлении обычно на 30–66,7% больше, чем при постоянном объеме. Следовательно коэффициент теплоемкости газов обычно составляет от 1,3 до 1,67.
Применимость
Удельную теплоемкость можно определить и измерить для газов, жидкостей и твердых тел довольно общего состава и молекулярной структуры. К ним относятся газовые смеси, растворы и сплавы или гетерогенные материалы, такие как молоко, песок, гранит и бетон, если рассматривать их в достаточно большом масштабе.
Удельная теплоемкость также может быть определена для материалов, которые изменяют состояние или состав при изменении температуры и давления, если изменения обратимы и постепенны. Таким образом, например, концепции могут быть определены для газа или жидкости, которые диссоциируют при повышении температуры, до тех пор, пока продукты диссоциации быстро и полностью рекомбинируют при падении.
Удельная теплоемкость не имеет значения, если вещество претерпевает необратимые химические изменения или если есть изменение фазы, например, плавление или кипение при резкой температуре в диапазоне температур, охватываемых измерением.
Теплоотдача и терморегуляция
Количество
теплоты Q,
переносимое вследствие теплопроводности
за время Δt,
определяется формулой
Q=k1ΔTΔSΔt/Δx
где
k1—
коэффициент теплопроводности; ΔT/Δx
— градиент тем-
пературы
в направлении, перпендикулярном площадке
ΔS.
Количество
теплоты Q,
переносимое вследствие конвекции за
время Δt,
определяется формулой;
Q=k2(T-T)ΔSΔt
где
k2
— коэффициент теплопередачи при
конвекции; Т и Т
— соответственно
температуры поверхности ΔS
и омываемой среды.
Количество
теплоты Q,
излучаемое за время Δt
абсолютно черным телом, определяется
формулой (закон Стефана — Больцмана)
Q=σT4ΔSΔt
где
σ—
постоянная Стефана — Больцмана; Т
— абсолютная температура
тела; ΔS
— площадь излучающей поверхности тела.
Для
реальных физических тел закон Стефана
— Больцмана имеет
вид
Q=k3σT4ΔSΔt
где
k3
— коэффициент, учитывающий, что свойства
поверхности реальных
физических тел отличны от свойств
поверхности абсолютно
черного тела (k3<. k>3=
1.
При
наличии двух встречных потоков радиации
от излучающей
поверхности к среде и от среды к
поверхности закон Стефана
— Больцмана имеет вид
Q=k3σ(T4–T4)ΔSΔt
где
Т и Т
— абсолютные температуры тела и
среды; ΔS
— площадь
излучающей поверхности тела.
Длина
волны λт,
которой соответствует максимум
излуча-тельной способности черного
тела, обратно пропорциональна абсолютной
температуре Т (закон смещения Вина):
λm=b/T
где
b
— постоянная закона смещения Вина.
Рекомендации
- Открытый университет (2008 г.). S104 Книга 3 Энергия и свет, п. 59. Открытый университет. ISBN .
- Открытый университет (2008 г.). S104 Книга 3 Энергия и свет, п. 179. Открытый университет. ISBN .
- Справочник Ланге по химии, 10-е изд. стр. 1524
- Издается под эгидой Verein Deutscher Ingenieure (VDI).
- Фейнман Р. Лекции по физике. I, глава 40, стр. 7-8
- Чарльз Киттель; Герберт Кремер (2000). Теплофизика. Фримен. п. 78. ISBN 978-0-7167-1088-2.
- Стивен Т. Торнтон и Эндрю Рекс (1993): Современная физика для ученых и инженеров, Saunders College Publishing, 1993 г.
- М.В. Чейз-младший (1998) , В Журнал физических и химических справочных данных, Монография 9, страницы 1-1951.
- Ричард Фейнман, Лекции по физике, Том 1 (45)
- Юнус А. Ценгель и Майкл А. Боулс, Термодинамика: инженерный подход, 7-е издание, McGraw-Hill, 2010, ISBN 007-352932-X.
Теплоемкости при постоянном давлении и постоянном объеме
При сообщении телу некоторого количества теплоты изменяется его температура (за исключением агрегатных превращений и вообще изотермических процессов). Характеристиками такого изменения являются различные теплоемкости: теплоемкость тела CT, удельная теплоемкость вещества c, молярная теплоемкость C.
Понятия теплоемкости тела и удельной теплоемкости рассмотрены тут.
Молярная теплоемкость C — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:
Единицей молярной теплоемкости в СИ является джоуль на моль-Кельвин (Дж/моль·К).
Удельная теплоемкость связана с молярной соотношением
В отличие от такой, например, характеристики вещества, как его молекулярная масса Mr удельная теплоемкость вещества не является неизменным параметром. Удельная теплоемкость может резко изменяться при переходе вещества из одного агрегатного состояния в другое. Так, вода в газообразном состоянии имеет удельную теплоемкость 2,2·103 Дж/кг·К а в жидком 4,19·103 Дж/кг·К .
Теплоемкость зависит и от условий, при которых происходит передача теплоты телу. Последнее особенно относится к газам. Например, при изотермическом расширении газа ему передается некоторое количество теплоты Q > 0, а ΔΤ = 0. Следовательно, удельная теплоемкость газа при изотермическом процессе
При адиабатном сжатии (расширении) газ не получает теплоты и не передает ее окружающим телам (Q = 0), а температура газа изменяется (ΔΤ ≠ 0). Следовательно, удельная теплоемкость газа при адиабатном процессе
Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или при постоянном давлении. В первом случае теплоемкость называется теплоемкостью при постоянном объеме или изохорной теплоемкостью (cV, CV), во втором — теплоемкостью при постоянном давлении или изобарной теплоемкостью (cp, Cp).
Если объем не изменяется (ΔV = 0), то работа, совершенная газом, так же равна нулю (А = 0). Согласно первому закону термодинамики
Откуда
Следовательно, теплоемкость при постоянном объеме равна изменению внутренней энергии газа при изменении температуры на 1 К.
Если газ идеальный, то в формуле (2)
Тогда молярная теплоемкость при постоянном объеме \(~C_V = \frac{\Delta U_M}{\Delta T}\), где \(~\Delta U_M = \frac i2 R \Delta T\) — изменение внутренней энергии 1 моль газа. Из этих равенств теплоемкость газа при постоянном объеме — \(~C_{TV} = \frac i2 \frac mM R\); молярная теплоемкость газа при постоянном объеме — \(~C_V = \frac i2 R\).
Если газ нагревается при постоянном давлении, то согласно первому закону термодинамики
где \(~A = p \Delta V = \frac mM R \Delta T\).
Тогда теплоемкость газа при постоянном давлении
Молярная теплоемкость при постоянном давлении:
Таким образом, теплоемкость при постоянном давлении всегда больше теплоемкости при постоянном объеме. Их отношение равно
где γ — показатель адиабаты (коэффициент Пуассона).
Из-за малости величины коэффициента объемного расширения твердых и жидких тел работой, совершаемой ими при нагревании при постоянном давлении, можно пренебречь и считать, что теплоемкости при постоянном объеме и постоянном давлении практически совпадают. Поэтому теплоемкость твердых и жидких тел при заданной температуре может считаться вполне определенной величиной.
AISI 304
Обозначение по международным стандартам
| Температура, ºC | Сталь 20 | Сталь 40 | Температура, ºC | Сталь 20 | Сталь 40 |
| 50 – 100 | 486 | 486 | 700 – 750 | 1433 | 1584 |
| 100 – 150 | 507 | 503 | 750 – 800 | 951 | 624 |
| 150 – 200 | 520 | 515 | 800 – 850 | 737 | 503 |
| 200 – 250 | 532 | 528 | 850 – 900 | 649 | 549 |
| 250 – 300 | 557 | 549 | 900 – 950 | 649 | 624 |
| 300 – 350 | 574 | 570 | 950 – 1000 | 649 | 624 |
| 350 – 400 | 599 | 587 | 1000 – 1050 | 649 | 633 |
| 400 – 450 | 624 | 612 | 1050 – 1100 | 649 | 633 |
| 450 – 500 | 662 | 649 | 1100 – 1150 | 658 | 641 |
| 500 – 550 | 704 | 691 | 1150 – 1200 | 666 | 654 |
| 550 – 600 | 750 | 708 | 1200 – 1250 | 679 | 670 |
| 600 – 650 | 788 | 733 | 1250 – 1300 | 687 | 687 |
| 650 – 700 | 846 | 771 | |||
| Температура, ºC | Сталь 20 | Сталь 40 | Температура, ºC | Сталь 20 | Сталь 40 |
| 100 | 486 | 486 | 750 | 679 | 670 |
| 150 | 494 | 494 | 800 | 675 | 704 |
| 200 | 499 | 503 | 850 | 662 | 704 |
| 250 | 507 | 511 | 900 | 658 | 704 |
| 300 | 515 | 520 | 950 | 654 | 700 |
| 350 | 524 | 528 | 1000 | 654 | 696 |
| 400 | 532 | 541 | 1050 | 654 | 691 |
| 450 | 545 | 549 | 1100 | 649 | 691 |
| 500 | 557 | 561 | 1150 | 649 | 691 |
| 550 | 570 | 574 | 1200 | 649 | 687 |
| 600 | 582 | 591 | 1250 | 654 | 687 |
| 650 | 595 | 608 | 1300 | 654 | 687 |
| 700 | 608 | 629 |
| Международный стандарт | Американский ASTM A240 | Европейский ЕN 10088-2 | Российский ГОСТ 5632-72 |
| Обозначение марки | AISI 304 | 1.4301 | 08Х18Н10 |
| 12Х18Н9 |
Применяемые стандарты и одобрения
AMS 5513 ASTM A 240 ASTM A 666
Применение
- Предметы домашнего обихода
- Раковины
- Каркасы для металлоконструкций в строительной промышленности
- Кухонная утварь и оборудование для общепита
- Молочное оборудование, пивоварение
- Сварные конструкции
- Резервуары судовые и наземные танкеры для продовольствия, напитков и некоторых химических веществ
Обычно производители стали разделяют марку на три основных класса (сорта) по способности к волочению:
- AISI 304 – Основной сорт
- AISI 304 DDQ (Normal and deep drawing) – Сорт глубокой вытяжки
- AISI 304 DDS (Extra deep drawing) – Сорт особо глубокой вытяжки
Механические свойства
| AISI 304 | Сопротивление на разрыв (σв), Н/мм² | Предел текучести(σ0,2), Н/мм² | Предел текучести(σ1,0), Н/мм² | Относительное удлинение (σ), % | Твердость по Бринеллю (HB) | Твердость по Роквеллу (HRB) |
| В соответствии с EN 10088-2 | ≥520 | ≥210 | ≥250 | ≥45 | – | – |
| В соответствии с ASTM A 240 | ≥515 | ≥205 | – | ≥40 | 202 | 85 |
Механические свойства при высоких температурах
Все эти значения относятся к только AISI 304
Физические свойства
| Физические свойства | Условные обозначения | Единица измерения | Температура | Значение |
| Плотность | d | – | 4°C | 7.93 |
| Температура плавления | °C | 1450 | ||
| Удельная теплоемкость | c | J/kg.K | 20°C | 500 |
| Тепловое расширение | k | W/m.K | 20°C | 15 |
| Средний коэффициент теплового расширения | α | 10 -6 .K -1 | 0-100°C 0-200°C | 17.5 18 |
| Электрическое удельное сопротивление | ρ | Ωmm 2 /m | 20°C | 0.80 |
| Магнитная проницаемость | μ | в 0.80 kA/m DC или в/ч AC | 20°C μ μ разряж.возд. | 1.02 |
| Модуль упругости | E | MPa x 10 3 | 20°C | 200 |
Сопротивление коррозии
304-е стали имеют хорошее сопротивление к общим коррозийным средам, но не рекомендованы там, где есть риск межкристаллитной коррозии. Они хорошо приспособлены для эксплуатации в пресной воде и городской и сельской среде. Во всех случаях необходима регулярная очистка внешних поверхностей для сохранения их первоначального состояния.
304-е стали имеют хорошее сопротивление различным кислотам:
- фосфорной кислоте во всех концентрациях при температуре окружающей среды,
- азотной кислоте до 65 % при температуре 20°C – 50°C,
- муравьиной и молочной кислоте при комнатной температуре,
- уксусной кислоте при температуре 20°C – 50°C.
Их рекомендуют для производства оборудования, контактирующего с холодными или горячими пищевыми продуктами: вино, пиво, молоко (кисломолочные продукты), спирт, натуральные плодовые соки, сиропы, патока, и т.д.
Кислотные среды
| Температура, °C | 20 | 80 | ||||||||||
| Концентрация, % к массе | 10 | 20 | 40 | 60 | 80 | 100 | 10 | 20 | 40 | 60 | 80 | 100 |
| Серная кислота | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | |
| Азотная кислота | 2 | 1 | 2 | |||||||||
| Фосфорная кислота | 2 | 1 | 2 | |||||||||
| Муравьиная кислота | 1 | 2 | 2 | 1 |
Код: 0 = высокая степень защиты – Скорость коррозии менее чем 100мкм/год 1 = частичная защита – Скорость коррозии от 100 до 1000мкм/год 2 = нет защиты – Скорость коррозии более чем 1000мкм/год
Атмосферные воздействия
Сравнение 304-й
марки с другими металлами в различных окружающих средах (Скорость коррозии расчитана при 10-летнем воздействии).
| Окружающая среда | Скорость коррозии (мкм/год) | ||
| AISI 304 | Алюминий-3S | Углеродистая сталь | |
| Сельская | 0.0025 | 0.025 | 5.8 |
| Морская | 0.0076 | 0.432 | 34.0 |
| Индустриальная Морская | 0.0076 | 0.686 | 46.2 |
Устойчивость к коррозии в кипящих химикалиях
| Кипящая среда | Состояние металла | Скорость коррозии (мм/год) |
| 20%-ая уксусная кислота | Обычный металл Сваренный | * (При толщине образца 0.8 мм и диаметре пресса равном 20 мм) |
| AISI 430 | 2.05 мм | |
| AISI 304 | 2.0 мм |
*Limiting drawing ratio – предельный коэффициент вытяжки
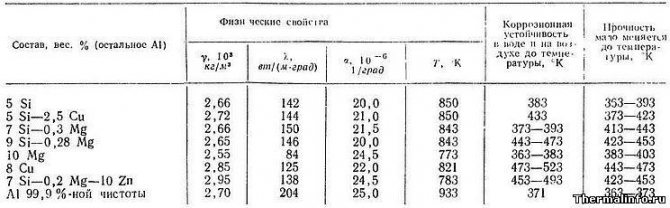
Свойства сплавов алюминия с кремнием, медью, магнием и цинком
В таблице представлены состав и следующие теплофизические свойства алюминиевых сплавов:
- плотность сплавов, кг/м3;
- коэффициент теплопроводности, Вт/(м·°С);
- коэффициент линейного теплового расширения, 1/град;
- коррозионная устойчивость в воде и на воздухе;
- температура изменения прочности.
Плотность, теплопроводность и коэффициент линейного теплового расширения сплавов представлены в зависимости от температуры в интервале от 500 до 660°С. Плотность алюминиевых сплавов с кремнием и цинком наиболее высока. Из легких сплавов можно отметить сплавы, содержащие магний.
Следует отметить, что наибольшей коррозионной устойчивостью в воде и на воздухе обладают алюминиевые сплавы с высоким содержанием меди — они устойчивы к коррозии до температуры 200…250°С. Такие сплавы также обладают высокими прочностными характеристиками.
Краткая теория и методика выполнения работы
Удельной
теплоемкостью
вещества называется величина, равная
количеству теплоты, которую необходимо
сообщить единице массы вещества для
увеличения ее температуры на один градус
Кельвина:
. (4.1)
Теплоемкость
одного моля вещества называется молярной
теплоемкостью:
, (4.2)
где
m – масса, µ – молярная масса вещества,– число молей газа.
Значение
теплоемкости газов зависит от условий
их нагревания. В соответствии с первым
законом термодинамики количество
теплоты,
сообщенное системе, расходуется на
увеличение ее внутренней энергиии на совершение системой работыпротив внешних сил:
. (4.3)
Изменение
внутренней энергии идеального газа в
случае изменения его температурыравно:
, (4.4)
здесь
– число степеней свободы молекулы газа,
под которым подразумевается число
независимых координат, полностью
определяющих положение молекулы в
пространстве;– универсальная газовая постоянная.
При
расширении газа система совершает
работу:
. (4.5)
Если
газ нагревать при постоянном объеме
(),
тои, согласно (4.3), все полученное газом
количество теплоты расходуется только
на увеличение его внутренней энергии.
Следовательно, учитывая (4.4), молярная
теплоемкость идеального газа при
постоянном объеме будет равна:
. (4.6)
Если
газ нагревать при постоянном давление
(),
то полученное газом количество теплоты
расходуется на увеличение его внутренней
энергиии совершение газом работы:
.
Тогда
молярная теплоемкость идеального газа
при постоянном давлении определяется
следующим образом:
. (4.7)
Используя
уравнение состояния идеального газа
(уравнение Клапейрона–Менделеева),
можно показать, что для одного моля газа
справедливо соотношение:
,
поэтому:
.
Последнее выражение
называют уравнением Майера. Из него,
учитывая (4.6), получаем:
. (4.8)
Отношение
теплоемкостейобозначаюти называют показателем адиабаты или
коэффициентом Пуассона:
. (4.9)
Адиабатным
называется процесс, протекающий в
термоизолированной системе, т.е. без
теплообмена с окружающей средой,.
На
практике он может быть осуществлен в
системе, окруженной теплоизоляционной
оболочкой, но поскольку для теплообмена
необходимо некоторое время, то адиабатным
можно считать также процесс, который
протекает так быстро, что система не
успевает вступить в теплообмен с
окружающей средой.
Первый
закон термодинамики для адиабатного
процесса имеет вид.
Знак минус говорит о том, что при
адиабатном процессе система может
совершать работу только за счет внутренней
энергии. С учетом (4.4)–(4.6) имеем:
. (4.10)
Продифференцировав
уравнение Клапейрона–Менделеева,
получим:
.
Выразим
из негои подставим в формулу (4.10):
.
Выразивиз уравнения Майера и учитывая соотношение
(4.8), получим:
.
Интегрируя
данное дифференциальное уравнение при
условииполучим выражение:
.
(4.11)
Уравнение
(4.11) называется уравнением адиабаты или
уравнением Пуассона.
Метод
определения показателя адиабаты,
предложенный Клеманом и Дезормом (1819
г.), основывается на изучении параметров
некоторой массы газа, переходящей из
одного состояния в другое двумя
последовательными процессами –
адиабатным и изохорным. Эти процессы
на диаграмме–(рис. 4.1) изображены кривыми соответственно
1–2 и 2–3.
Если
в сосуд, соединенный с дифференциальным
датчиком давления, накачать воздух и
подождать до установления теплового
равновесия с окружающей средой, то в
этом начальном состоянии 1 газ имеет
параметры,,,
причем температура газа в сосуде равна
температуре окружающей среды,
а давлениенемного больше атмосферного.
Если
теперь на короткое время соединить
сосуд с атмосферой, то произойдет
адиабатное расширение воздуха. При этом
воздух в сосуде перейдет в состояние
2, его давление понизится до атмосферного.
Масса воздуха, оставшегося в сосуде,
которая в состоянии 1 занимала часть
объема сосуда, расширяясь, займет весь
объем.
При этом температура воздуха, оставшегося
в сосуде, понизится до.
Поскольку процесс 1–2 – адиабатный, к
нему можно применить уравнение Пуассона
(4.11):
или.
Отсюда:
. (4.12)
После
кратковременного соединения сосуда с
атмосферой охлажденный из-за адиабатного
расширения воздух в сосуде будет
нагреваться (процесс 2–3) до температуры
окружающей средыпри постоянном объеме.
При этом давление в сосуде поднимется
до.
Поскольку
процесс 2–3 – изохорный, к нему можно
применить закон Шарля:
или
. (4.13)
Из уравнений (4.12)
и (4.13) получим:
.
Прологарифмируем
это выражение:
.
Поскольку
избыточные давленияиочень малы по сравнению с атмосферным
давлением,
а также учитывая, что при,
будем иметь:
.
Откуда:
. (4.14)
Избыточные
давленияиизмеряют с помощью дифференциального
датчика давления.
