Как найти коэффициент жёсткости пружины: формула, определение

Расчет в Excel жесткости витка пружины

Жесткость витка пружины – это «краеугольный камень в фундаменте» расчетов, зависящий лишь от модуля сдвига материала, из которого пружина навита и её геометрических размеров.

C 1 = G * X 4 /(Y *(D 1 — B ) 3 )

В этой формуле:

G – модуль сдвига материала проволоки

Для пружинной стали:

G ≈78500 МПа ±10%

Для пружинной бронзы:

G ≈45000 МПа ±10%

X – минимальный размер сечения проволоки

Для круглой проволоки – это её диаметр:

X = D

Для прямоугольной проволоки:

X = H при H B

X = B при B H

H – высота сечения проволоки в направлении параллельном оси навивки пружины

B – ширина сечения проволоки в направлении перпендикулярном оси навивки пружины

Для круглой проволоки:

H = B = D

D 1 — наружный диаметр пружины

(D 1 — B ) – средний диаметр пружины

Y – параметр жесткости сечения проволоки

Для круглой проволоки:

Y = 8

Для прямоугольной проволоки:

Y = f (H B )

Что это за функция — f (H B ) ? В литературе она всегда задана в виде таблицы, что не всегда удобно, особенно для промежуточных значений H B , которых попросту нет.

Выполним в MS Excel табличных данных в первых двух столбцах аналитическими функциями, разбив для повышения точности табличные значения на три группы.

На графиках, представленных ниже, Excel нашел три уравнения для определения параметра Y при различных значениях аргумента — отношения высоты проволоки к ширине — H B . Красные точки – это заданные значения из таблицы (столбец №2), черные линии – это графики найденных аппроксимирующих функций. Уравнения этих функций Excel вывел непосредственно на поля графиков.

В таблице в столбце №3 размещены посчитанные по полученным формулам значения параметра жесткости сечения проволоки Y , а в столбцах №4 и №5 — абсолютные Δ абс и относительные Δ отн погрешности аппроксимации.

Как видно из таблицы и графиков полученные уравнения весьма точно замещают табличные данные! Величина достоверности аппроксимации R 2 очень близка к 1 и относительная погрешность не превышает 2,7%!

Применим на практике полученные результаты.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина \(L_{0}\) пружины.

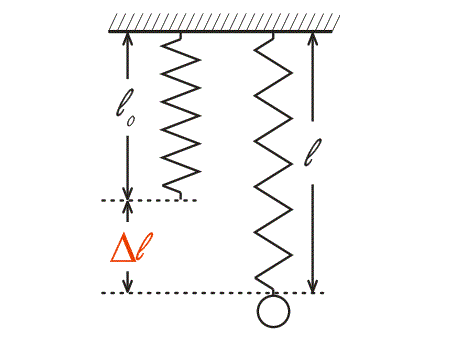Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение

Подвесим теперь к пружине груз. Пружина будет иметь длину \(L\), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

\

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину \(L_{0}\).

\

\( L_{0} \left(\text{м} \right) \)  – начальная длина пружины;

\( L \left(\text{м} \right) \)  – конечная длина растянутой пружины;

\( \Delta L \left(\text{м} \right) \)  – кусочек длины, на который растянули пружину;

Величину \( \Delta L \) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

\

\( \varepsilon \) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Зачем требуется маркировка цветом

Цветная маркировка, упрощающая жизнь автолюбителям при выборе, является следствием сложного процесса производства. Он характеризуется огромным количеством сложных технологических операций, которые очень трудно, а зачастую и невозможно, проконтролировать.

Поэтому все производители, осуществляющие массовый выпуск пружин, после изготовления считают необходимым проводить сравнительные анализы продукции. В результате этого появилась классификация по цвету, поскольку только так можно отличить разные по жесткости элементы после изготовления. Конечно, существуют и другие способы определить пружины разных видов, но этот самый простой и надежный.

Расчет жесткости цилиндрической пружины

Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.

Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.

Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями «цилиндров», диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.

При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние «цилиндры» при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:

• $R$ — радиус цилиндра пружины,
• $n$ — количество витков проволоки радиуса $r$,
• $G$ — коэффициент, зависящий от материала.

Рассчитать коэффициент жесткости пружины, выполненной из стальной проволоки с $G = 8 cdot 10^<10>$ Па и диаметром 1 мм. Радиус пружины 20 мм, количество витков – 25.

Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:

Ответ: $100 frac<Н><м>$

Так и не нашли ответ на свой вопрос?

Просто напиши с чем тебе нужна помощь

Основные характеристики

Независимо от вида пружин, особенности их работы, связанные с постоянно деформацией, требуют наличия таких параметров:

• Способности сохранять постоянное значение упругости в течение заданного срока.
• Пластичности.
• Релаксационной стойкости, благодаря которой деформации не становятся необратимыми.
• Прочности, то есть способности выдерживать различные виды нагрузок: статические, динамические, ударные.

Каждая из этих характеристик важна, однако при выборе упругой комплектующей для конкретной работы в первую очередь интересуются ее жесткостью как важным показателем того, подойдет ли она для этого дела и насколько долго будет работать.

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆ l ( l ₁ – l , где l — начальная длина, l ₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

В формуле используется коэффициент k . Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F_упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние – в метрах. Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них)

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F_упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Суть метода заключается в том, что пружину нагружают силой определенной величины (в нашем случае, вес груза)

Дожидаются наступления статического равновесия пружины и замеряют ее деформацию под воздействием этой силы

Величина коэффициента жесткости

Далее определяются максимальное ( ) и минимальное ( ) значения коэффициента жесткости по следующим принципам

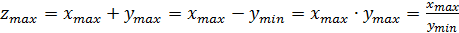, (12)

, (13)

где , , , , , – максимальные и минимальные значения величин, задействованных в формулах.

Затем, поскольку коэффициент жесткости распределяется по симметричному «нормальному закону», по формулам, приведенным ниже для величин, определяются среднее значение коэффициента жесткости, половина доверительного интервала и относительная погрешность результата

(14)

(15)

. (16)

Определение коэффициента жесткости пружины методом строительной механики

Коэффициент жесткости определяется по зависимости

. (17)

С использованием формулы 17, а также зависимостей 12 и 13 определяются максимальное ( ) и минимальное ( ) значения коэффициента жесткости.

Затем, по формулам 14, 15 и 16 определяются среднее значение коэффициента жесткости, половина доверительного интервала и относительная погрешность результата.

ИТОГИ ЛАБОРАТОРНОЙ РАБОТЫ И ОФОРМЛЕНИЕ ОТЧЕТА

Итоги лабораторной работы

Анализируя полученные результаты необходимо сравнить методы определения коэффициента жесткости по критериям точности и сложности. Далее, дать оценку точности и достоверности полученных результатов, а также предложить меры по повышению точности результатов в случае неудовлетворительности последних.

Оформление отчета

Оформляется один отчет на бригаду на листах формата А4.

В отчете должны быть приведены все необходимые данные, расчеты и пояснения, результаты и выводы.

Отчет должен содержать следующие обязательные элементы: титульный лист с фамилиями выполнявших работу и проверяющего, оглавление с указанием номеров страниц начала разделов, нумерацию страниц, и разделы в следующем порядке:

1) исходные данные (см. п. 2.3),

2) определение статистических оценок измеренных величин,

3) определение коэффициента жесткости пружины статическим методом,

4) определение коэффициента жесткости пружины методом строительной механики,

Все появляющиеся первый раз переменные должны быть сопровождены пояснениями. Например,

деформация пружины – или

или

–модуль упругости стали при сдвиге.

У всех значений величин, имеющих размерность, должны стоять соответствующие единицы измерения. Все формулы должны быть раскрыты и сосчитаны. Например,

=176-138=38 мм.

Все рисунки и таблицы должны иметь названия и сквозную нумерацию.

СПИСОК ЛИТЕРАТУРЫ

1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1962. – 576 с.

2. ГОСТ 24026-80 Исследовательские испытания. Планирование эксперимента. Термины и определения.

3. Налимов В. В. Теория эксперимента – М.: Наука, 1971. – 207 с.

4. Румшиский Л.3. Математическая обработка результатов эксперимента – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1971. – 192 с.

Приложение

	0.9	0.95	0.98	0.99	0.999
2.132	2.776	3.747	4.604	8.610
2.015	2.571	3.365	4.032	6.859
1.943	2.447	3.143	3.707	5.959
1.895	2.365	2.998	3.499	5.405
1.860	2.306	2.896	3.355	5.041
1.833	2.262	2.821	3.250	4.781
1.812	2.228	2.764	3.169	4.587
1.796	2.201	2.718	3.106	4.487
1.782	2.179	2.681	3.055	4.318
1.771	2.160	2.650	3.012	4.221
1.761	2.145	2.624	2.977	4.140
1.753	2.131	2.602	2.947	4.073
1.746	2.120	2.583	2.921	4.015
1.734	2.103	2.552	2.878	3.922
1.725	2.086	2.528	2.845	3.850
1.708	2.060	2.485	2.787	3.725
1.697	2.042	2.457	2.750	3.646
1.689	2.030	2.437	2.724	3.591
1.684	2.021	2.423	2.704	3.551
1.679	2.014	2.412	2.689	3.522
1.676	2.008	2.403	2.677	3.497
1.671	2.000	2.390	2.660	3.460
1.667	1.995	2.381	2.648	3.436
1.664	1.990	2.374	3.639	3.416
1.662	1.987	2.368	2.632	3.401
1.660	1.984	2.364	2.626	3.391
	1.645	1.960	2.326	2.576	3.291

Учебно-методическое пособие по выполнению расчетных работ

Одерышев Андрей Васильевич

ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ

Печатается в авторской редакции

Подписано в печать Сдано в производство

Формат 1/16 Усл.-печ. л. Уч.-изд. л. 2.

Тираж 100 экз. Заказ №

Государственный университет морского и речного флота им. адм. С.О. Макарова,

198035, Санкт-Петербург, улица Двинская, 5/7

Отпечатали в типографии ФБОУ ВПО ГУМРФ

198035, Санкт – Петербург, Межевой канал, 2

Последовательное соединение пружин

При последовательном соединении двух пружин, имеющих коэффициенты жесткости с

1,с 2 (рис. 2.6), смещение тела равно сумме деформаций пружин:

. (2.11)

Рис. 3.6 Последовательное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с

* будет равна каждой из сил упругости установленных пружин, откуда

,

,

Окончательно с учетом (2.11) получаем

. (2.12)

Влияние сопротивления на свободные колебания

Пусть на точку массы m

, совершающую прямолинейное движение, действуют две силы (рис. 2.7):

Восстанавливающая сила (сила упругости пружины):

.

Сила сопротивления, пропорциональная скорости движения точки (сила сопротивления демпфера):

.

Рис. 2.7 Движение массы с демпфированием

Дифференциальное уравнение движения точки запишется как

;

,

,

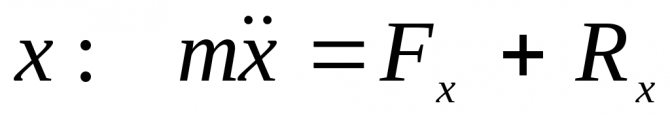
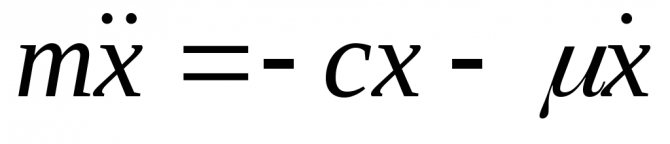
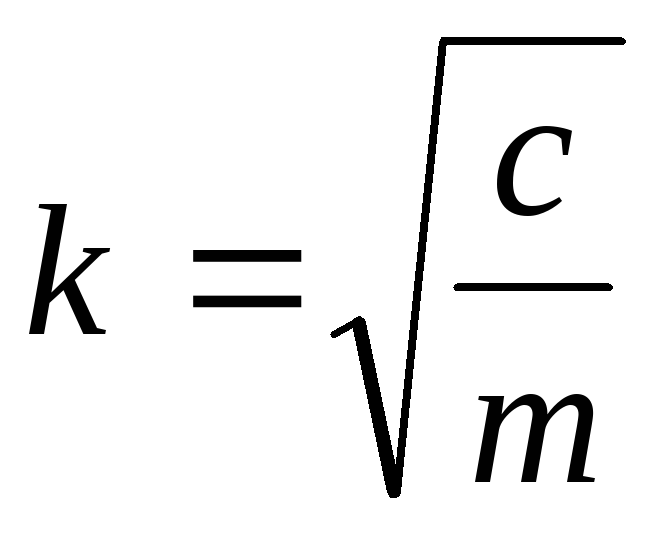
, (2.13)

получаем линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

. (2.14)

Характеристическое уравнение имеет вид

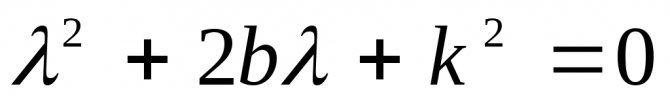
, (2.15)

его корни равны

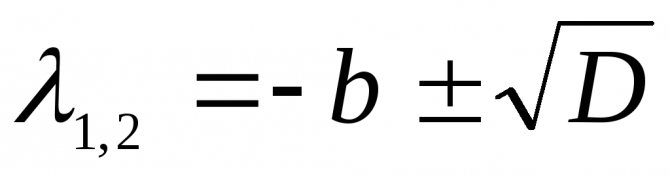
, (2.16)

где

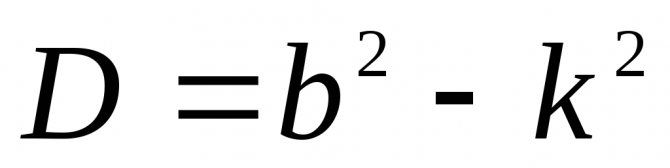
– дискриминант.

Как известно из курса высшей математики, общее решение дифференциального уравнения (2.14) существенно зависит от знака дискриминанта

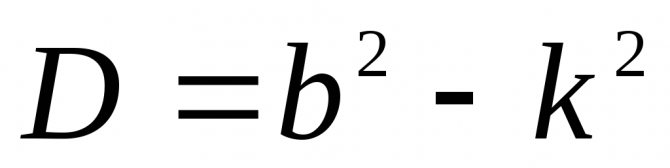
, т.е. от соотношения между b

иk. 1-й случай (малое сопротивление): b

k,D  0.

Обозначим

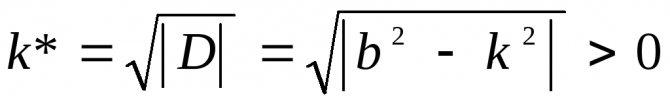
, причем k*

k . Тогда корни (2.16) характеристического уравнения будут комплексно сопряженными:

,

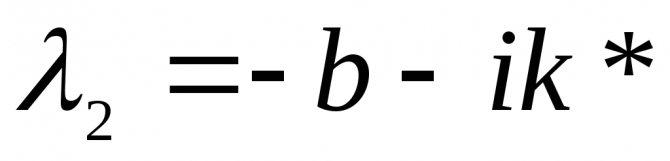
Общее решение дифференциального уравнения (2.14) в данном случае имеет вид

, (2.17)

это затухающие колебания с частотой k* и периодом

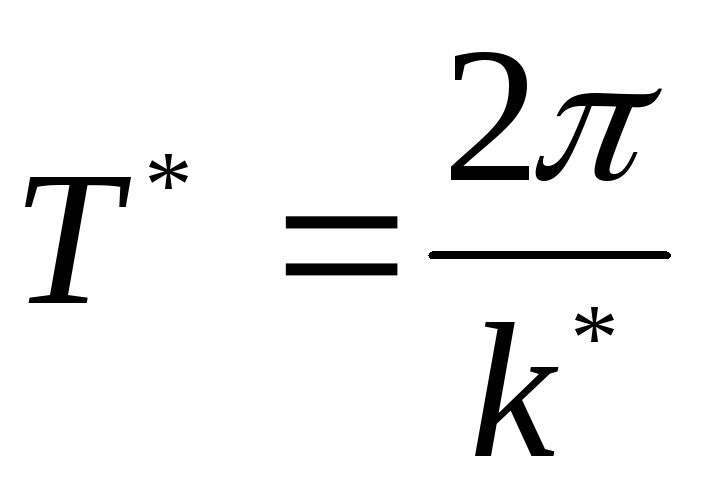
(рис.3.8).

Амплитуда колебаний убывает со временем. Отношение последующей амплитуды к предыдущей называется декрементом затухания:

*

k ) и к увеличению их периода (Т* >Т ).

Корни (2.16) характеристического уравнения получаются кратные,

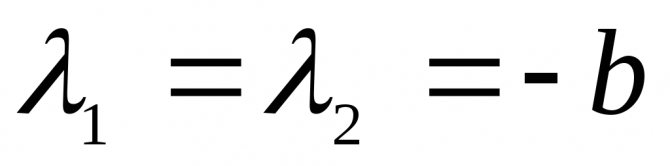
, и решение дифференциального уравнения (2.14) приобретает вид

. (2.19)

Поскольку экспонента убывает быстрее, чем растёт линейная функция времени, в зависимости от начальных условий движения получим ту или иную картину затухающего апериодического (т.е. не колебательного) движения (рис.2.9).

3-й случай (большое сопротивление): b>k ,D > 0.

В этом случае обозначим

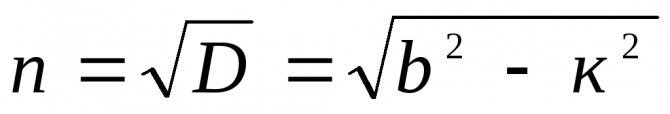
>0, и оба корня (2.16) характеристического уравнения будут действительными и отрицательными:

Практические занятия

Механики и физики обозначают с помощью k, c и D коэффициент упругости, пропорциональности, жесткости. Смысл математической записи одинаковый. Численно показатель равняется силе, которая создаёт колебания на одну единицу длины. На практических работах по физике используется в качестве последней величины 1 метр.

Чем выше k, тем больше сопротивление предмета относительно деформации. Дополнительно коэффициент показывает степень устойчивости тела к колебаниям со стороны внешней нагрузки. Параметр зависит от длины и диаметра винтового изделия, количества витков, сырья. Единица измерения жесткости пружины — Н/м.

На практике перед школьниками и механиками может стоять более сложная задача, к примеру, найти общую жёсткость. В таком случае пружины соединены последовательным либо параллельным способом. В первом случае уменьшается суммарная жесткость. Если пружины расположены последовательно, используется следующая формула: 1/k = 1/k1 + 1/k2 + … + 1/ki, где:

• k — суммарная жёсткость соединений;
• k1 …ki — жёсткость каждого элемента системы;
• i — число пружин в цепи.

Если невесомые (расположены горизонтально) предметы соединены параллельно, значение общего k будет увеличиваться. Величина вычисляется по следующей формуле: k = k1 + k2 + … + ki.

Основная методика для вычислений

На практике коэффициент Гука определяется самостоятельно. Для эксперимента потребуется пружина, линейка, груз с определённой массой. Необходимо соблюдать следующую последовательность действий:

1. Пружина фиксируется вертикально. Для этого используется любая удобная опора со свободной нижней частью.
2. Линейкой измеряется длина предмета. Результат записывается как х1.
3. На свободный конец подвешивается груз с известной массой m.
4. Измеряется длина изделия под воздействием амплитуды. Вывод записывается как х2.
5. Производит подсчёт абсолютного удлинения: x = x2-x1. Для определения энергии (силы) и k в международной системе СИ осуществляется перевод длины из разных единиц измерения в метры.
6. Сила, спровоцировавшая деформацию, считается силой тяжести тела. Она рассчитывается по формуле: F = mg, где м является массой используемого груза (вес переводится в килограммы), а g (равен 9,8) — постоянная величина, с помощью которой отмечается ускорение свободного падения.

Если вышеописанные вычисления произведены, необходимо найти значение коэффициента жёсткости. Используется закон Гука, из которого следует, что k=F/x.

Решение задач

Для нахождения жёсткости в случае использования разных предметов, включая пружинные маятники с разной частотой колебаний, применяется формула Гука либо следствие, вытекающее из неё.

Задача № 1. Пружина имеет длину 10 см. На неё оказывается сила в 100 Н. Изделие растянулось на 14 см. Нужно найти k.

Решение: предварительно вычисляется абсолютное удлинение: 14−10=4 см. Результат переводится в метры: 0,04 м. Используя основную формулу, находится k. Его значение равняется 2500 Н/м.

Задача № 2. На пружину подвешивается груз массой 10 кг. Изделие растягивается на 4 см. Нужно найти длину, на которую растянется пружина, если использовать груз массой в 25 кг.

Решение: Определяется сила тяжести путем умножения 10 кг на 9.8. Результат записывается в Ньютонах. Определяется k=98/0.04=2450 Н/м. Рассчитывается, с какой силой воздействует второй груз: F=mg=245 Н. Для нахождения абсолютного удлинения используется формула x=F/k. Во втором случае х равняется 0,1 м.

Формула определения жесткости

Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или

Читать также: Инструмент для установки резьбовых заклепок

равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).

Другой вариант записи формулы: коэффициент Юнга

Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.

Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.

К примеру, модуль Юнга для ста

ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).

Смысл понятия коэффициент жесткости

Коэффициент жесткости – коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.

Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).

Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:

• Материала, используемого при ее изготовлении.
• Формы и конструктивных особенностей.
• Геометрических размеров.

По этому показателю можно сд

елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.

Особенности расчета пружин

Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.

Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.

• Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
• При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.