Точность измерений и погрешности в физике — определение и формулы с примерами

Введение

Все, что сказано в этом введении, запоминать не нужно. это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.

1. Как определять погрешности измерений

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

A, B, C, … — физические величины.

A_пр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.

ΔA — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_иA — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; указывается в каждой работе при описании прибора в разделе Оборудование и средства измерения)

Δ_оA — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене деления секундомера или часов.

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

ΔA=Δ_иA + Δ_оA

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔA≈0,17=0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А=10,332≈10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.

В этом случае A_пр находят как среднее арифметическое значение всех измерений, а ΔA (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется, как показано в таблице 1.

Абсолютная погрешность косвенных измерений определяется по формуле ΔA=A_прε (ε выражается десятичной дробью).

Таблица 1

Формулы для нахождения относительной погрешности косвенных измерений

Nº п/п	Формула физической величины	Формула относительной погрешности
1
2
3	A=B+C
4

2. О классе точности электроизмерительных приборов

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иA от всей шкалы прибора (A_max):

Класс точности указывается при описании прибора в разделе Оборудование и средства измерения. Cуществуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (A_max), определяют абсолютную погрешность Δ_иA измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений

1. Записать результаты измерений в виде двойных неравенств:

A_{1 пр} – ΔA₁ < A_{1 пр} < A_{1 пр} + ΔA₁
A_{2 пр} – ΔA₂ < A_{2 пр} < A_{2 пр} + ΔA₂
2. Сравнить полученные интервалы значений (рис.1): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений.

Рисунок 1.

4. Как оформлять отчет о проделанной работе

Отчетом о проделанной работе является форма, находящаяся в левом нижнем окне. После ее заполнения надо нажать на кнопку «Отправить результаты на сервер».

Значения измеренных физических величин переносятся в таблицу результатов автоматически после нажатия соответствующей кнопки.

Значения остальных величин и ответ на контрольный вопрос вводятся с клавиатуры.

домашней странице BARSIC

Абсолютная погрешность — измерительный прибор

Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.
 

Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.
 

Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.
 

В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.
 

В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.
 

Суммарная погрешность

Зачастую в расчет принимается только погрешность измерительного прибора

Но также, дополнительно следует принимать во внимание погрешности измерительных инструментов, в том случае, если они используются. Вот несколько примеров:

Увеличение погрешности при использовании пробника 1:10

Если в процессе измерений используется щуп 1:10, то необходимо учитывать не только измерительную погрешность прибора. На погрешность также влияет входной импеданс используемого прибора и сопротивление щупа, которые вместе составляют делитель напряжения.

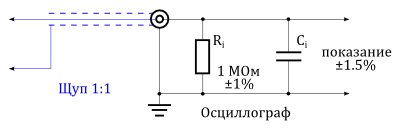
Подключенный к осциллографу щуп 1:1

На рисунке выше схематически показан осциллограф с подключенным к нему пробником 1:1. Если мы рассмотрим этот пробник как идеальный (нет сопротивления соединения), то приложенное напряжение передается прямо на вход осциллографа. Погрешность измерения теперь определяется только допустимыми отклонениями аттенюатора, усилителя и цепями, принимающими участие в дальнейшей обработке сигнала и задается производителем прибора. (На погрешность также влияет сопротивление соединения, которое формирует внутреннее сопротивление . Оно включается в заданные допустимые отклонения).

На рисунке ниже показан тот же самый осциллограф, но теперь ко входу подключен щуп 1:10. Этот пробник имеет  внутреннее сопротивление соединения и вместе со входным сопротивлением осциллографа образует делитель напряжения. Допустимое отклонение резисторов в делителе напряжения является причиной его собственной погрешности.

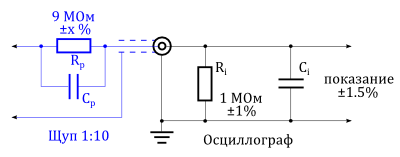
Пробник 1:10, подключенный к осциллографу, вносит дополнительную погрешность

Допустимое отклонение входного сопротивления осциллографа может быть найдено в его спецификации. Допустимое отклонение сопротивления соединения щупа не всегда дано. Тем не менее, погрешность системы заявляется производителем определенного осциллографического пробника для конкретного типа осциллографа. Если щуп используется с другим типом осциллографа, нежели рекомендуемый, то измерительная погрешность становится неопределенной. Этого нужно всегда стараться избегать.

Предположим, что осциллограф имеет допустимое отклонение 1.5% и используется щуп 1:10 с погрешностью в системе 2.5%. Эти две характеристики можно перемножить для получения полной погрешности показания прибора:

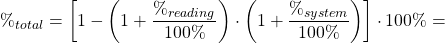
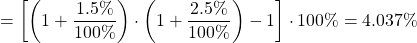
Здесь  — полная погрешность измерительной системы,  — погрешность показания прибора,  — погрешность щупа, подключенного к осциллографу, подходящего типа.

Измерения с шунтирующим резистором

Часто при измерениях токов используют внешний шунтирующий резистор. Шунт имеет некоторое допустимое отклонение, которое влияет на измерение.

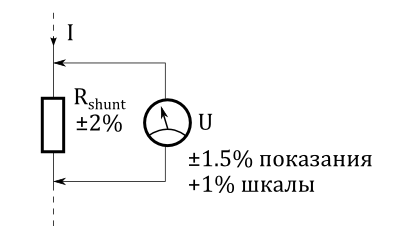
Увеличение погрешности при использовании шунтирующего резистора

Заданное допустимое отклонение шунтирующего резистора влияет на погрешность показания. Для нахождения полной погрешности, допустимое отклонение шунта и погрешность показаний измерительного прибора перемножаются:

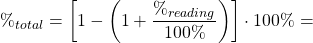
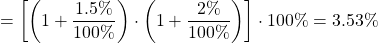
В этом примере, полная погрешность показания равна 3.53%.

Сопротивление шунта зависит от температуры. Значение сопротивления определяется для данной температуры. Температурную зависимость часто выражают в .

Для примера вычислим значение сопротивления для температуры окружающей среды . Шунт имеет характеристики: Ом (соответственно и ) и температурную зависимость .

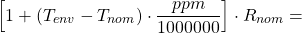
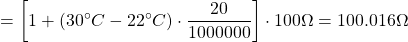
Ток, протекающий через шунт является причиной рассеяния энергии на шунте, что приводит к росту температуры и, следовательно, к изменению значения сопротивления. Изменение значения сопротивления при протекании тока зависит от нескольких факторов. Для проведения очень точного измерения, необходимо откалибровать шунт на дрейф сопротивления и условия окружающей среды при которых проводятся измерения.

Методы Корнфельда и Стьюдента

Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.

Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:

1. Предполагается, что имеется ряд результатов измерений от Х1 до Хn.
2. Из этих величин выбирают минимальную и максимальную.
3. Вычисляют среднее значение Х.
4. В пределах от наименьшего до наибольшего показателя выбирают доверительный интервал.
5. Чтобы найти абсолютное отклонение, необходимо вычесть из максимального результата измерения величину минимального. Полученную разность делят пополам.

Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.

Определение погрешности

Владельцев измерительных приборов интересует, прежде всего, величина максимальной погрешности, характерной для манометра. Она зависит не только от класса точности, но и от диапазона измерений. Таким образом, чтобы получить значение погрешности, нужно произвести некоторые вычисления. Например, для манометра с диапазоном измерений, равным 6 МПа, и классом точности 1,5 погрешность будет рассчитываться по формуле 6*1,5/100=0,09 МПа.

Необходимо отметить, что таким способом можно посчитать только основную погрешность.

Ее величина определяется идеальными условиями эксплуатации. На нее оказывают влияние только конструктивные характеристики, а также особенности сборки прибора, например, точность градуировки делений на шкале, сила трения в измерительном механизме. Однако эта величина может отличаться от фактической, поскольку существует также дополнительная погрешность, определяемая условиями, в которых эксплуатируется манометр. На нее может влиять вибрация трубопровода или оборудования, температура, уровень влажности и другие параметры.

Также точность измерения давления зависит от еще одной характеристики манометра — величины его вариации, которую определяют в ходе поверки. Это максимальная разница показаний измерителя, выявленная по результатам нескольких измерений.

Величина вариации в значительной мере зависит от конструкции манометра, а именно от способа уравновешивания, которое может быть жидкостным (давлением столба жидкости) или механическим (пружиной). Механические манометры имеют более выраженную вариацию, что часто обусловлено дополнительным трением при плохой смазке или износе деталей, потере упругости пружины и другими факторами.

Абсолютная и относительная погрешность

Абсолютной погрешностью или, короче, погрешностью приближенного
числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее)*.

Пример 1. На предприятии 1284 рабочих и служащих. При
округлении этого числа до 1300 абсолютная погрешность
составляет 1300 — 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 — 1280 = 4.

Относительной погрешностью приближенного числа называется отношение
абсолютной погрешности приближенного числа к самому этому числу.

Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная
погрешность составляет 200 — 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.

В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза
неизвестен. Но абсолютная погрешность не
превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈ 1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее
относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.

В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность — 1,4 %.

Величина предельной погрешности не является вполне определенной. Так, в примере 3 можно принять за предельную абсолютную
погрешность 100 г, 150 г и вообще всякое число, большее чем 50 г. На практике берется по возможности меньшее значение
предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно
предельной погрешностью. Для каждого приближенного числа должна быть известна его предельная погрешность
(абсолютная или oотносительная). Когда она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания
предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого
соглашения всегда можно обойтись без указания предельной погрешности числа.

Предельная абсолютная погрешность обозначается греческой буквой Δ («дельта»); предельная относительная
погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой а, то

δ = Δ/a.

Пример 4. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная
относительная погрешность этого измерения?
Здесь а = 17,9 см; можно принять Δ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, a значительно уменьшить, предельную погрешность ни удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша ребра могут разниться на бoльшую величину). Относительная погрешность равна 0,1/17,9.
Округляя, находим δ = 0,1/18 ≈ 0,6%.

Пример 5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы
предельная относительная погрешность составляла 0,05%?Решение. По условию, предельная абсолютная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная
абсолютная погрешность равна 36*(0,05/100) = 0,0175 (мм) или, усиливая, 0,02 (мм). Можно воспользоваться
формулой δ = Δ/a.
Подставляя в неё а = 35, δ = 0,0005, имеем 0,0005 = Δ/35. Значит, Δ = 35 • 0,0005 = 0,0175 (мм).

* Иначе говоря, если a есть приближенное число, а х – его точное значение, то абсолютная погрешность есть абсолютное
значение разности a – х. В некоторых руководствах абсолютной погрешностью называется сама
разность a – х (или разность х — a). Эта величина может быть положительной или отрицательной.

Точность

Термин точность используется для выражения случайности измерительной ошибки. Случайная природа отклонений измеряемых значений в большинстве случае имеет тепловую природу. Из-за случайной природы этого шума не возможно получить абсолютную ошибку. Точность дается только вероятностью того, что измеряемая величина лежит в некоторых пределах.

Распределение Гаусса

Тепловой шум имеет гауссово, или, как еще говорят, нормальное распределение. Оно описывается следующим выражением:

Здесь  — среднее значение, показывает дисперсию и соответствует RMS-значению шумового сигнала. Функция дает кривую распределения вероятностей, как показано на рисунке ниже, где среднее значение и эффективная амплитуда шума .

Распределение вероятностей с и

В таблице указаны шансы получения значений в заданных пределах.

Граница	Шанс
0.5·σ	38.3 %
0.674·σ	50.0 %
1·σ	68.3 %
2·σ	95.4 %
3·σ	99.7 %

Как видно, вероятность того, что измеренное значение лежит в диапазоне ± равна .

Повышение точности

Точность может быть улучшена передискретизацией (изменением частоты дискретизации) или фильтрацией. Отдельные измерения усредняются, поэтому шум значительно снижается. Также снижается разброс измеренных значений. Используя передискретизацию или фильтрацию необходимо учитывать, что это может привести к снижению пропускной способности.

Все о проверке

Теперь поговорим о том, как производится проверка манометров, какие сроки и периодичность проверяемых устройств и какие правила следует соблюдать.

Если поверка манометров осуществляется в лабораторных условиях, то по правилам она включает в себя следующие этапы:

• визуальная диагностика;
• выставление стрелки шкалы на нулевую метку;
• диагностика положения стрелки на этой метке;
• методика проверки включает в себя выявление основной погрешности.

Периодичность и сроки

Что касается периодичности, то на предприятиях обычно она вносится в соответствующий журнал проверки. Но поскольку рядовые автолюбители обычно не заводят журнал контрольных проверок манометров, эта информация может фиксироваться отдельно в блокноте. Периодичность диагностики может варьироваться в зависимости от производителя устройства, по правилам в среднем она может составлять от 12 до 60 месяцев (автор видео — канал Avtozvuk.ua — База Автозвука).

Инструкция по проверке манометра своими руками

Теперь вкратце о том, как проверить манометр своими силами. Перед тем, как приступить к измерению, необходимо произвести визуальную диагностику устройства. Внимательно осмотрите корпус на предмет наличия трещин, сколов, зазоров или других механических повреждений, которые могли бы привести к неработоспособности устройства. Если вы заметили следы повреждений, при этом прибор в принципе не работает, то его дальнейшая диагностика, вероятнее всего, будет бесполезной. Гораздо проще будет купить новое устройство, чем тратить время и ресурсы на ремонт старого.

Что касается непосредственно диагностики значений, то она осуществляется следующим образом:

1. Сначала необходимо продиагностировать давление, но для такой проверки вам понадобится так называемый эталонный девайс, то есть то устройство, в показаниях которого вы уверены. Если вы замеряете компрессию в цилиндрах силового агрегата или, к примеру, в шинах автомобиля, то измерьте давления сначала одним прибором, а затем — другим. В том случае, если показания вашего устройства не совпадают с эталонным, необходимо произвести его регулировку. Вам необходимо добиться того, чтобы показания от измерения с помощью двух устройств совпадали.
2. Чтобы выполнить настройку, на корпусе прибора должны располагаться специальные винты регулировки. Если вы используете электронное устройство, то принцип здесь, в целом, аналогичный, однако следует учитывать, что девайсы такого типа обладают инерционностью. Соответственно, показания надо будет удерживать от 8 до 10 с.
3. Если эталонный прибор у вас отсутствует, можно произвести диагностику правильности показаний, применив расчеты. Вам потребуется сосуд, об объеме которого вы знаете точно, причем воздух в нем находится при атмосферном давлении, уровень которого замеряется барометром, а температура должны быть комнатной. Сосуд следует плотно закрыть и немного нагреть, чтобы увеличились температура и давление, которые также следует измерить. Вам следует произвести расчет показания давления в самом сосуде, разделив конечную температура нагрева с изначальной, комнатной. После этого результат следует умножить на показатель атмосферного давления.
4. В том случае, если показатели устройства при такой температуре не совпадают с теми, которые были рассчитаны, необходимо произвести регулировку устройства таким образом, чтобы девайс показывал такое значение, которое получилось в ходе расчетов. Когда вы будете производить расчеты, учитывайте тот факт, что уровень температуры следует замерить к Кельвинах, а для этого к полученным градусам Цельсия следует добавить цифру 273. В большинстве случаев шкалы на приборах имеют градуировку в кг/см2, соответственно, расчет будет осуществлен в паскалях либо мм ртутного столба. Поэтому для получения более точных результатов необходимо будет перевести все единицы и только после этих действий производить сравнение.

Если регулировка не дает необходимых результатов и полученные показания прибора не являются верными, можно попробовать отдать устройство на диагностику специалистам. Но если и в лабораторных условиях не удалось получить нужный результат, то единственным выходом будет ремонт устройства либо его замена.

Загрузка …

ВЕСА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ

При неравноточных измерениях, когда результаты каждого измерения нельзя считать одинаково надежными, уже нельзя обойтись определением простого арифметического среднего. В таких случаях учитывают достоинство (или надежность) каждого результата измерений.Достоинство результатов измерений выражают некоторым числом, называемым весом этого измерения. Очевидно, что арифметическое среднее будет иметь больший вес по сравнению с единичным измерением, а измерения, выполненные при использовании более совершенного и точного прибора, будут иметь большую степень доверия, чем те же измерения, выполненные прибором менее точным.
Поскольку условия измерений определяют различную величину средней квадратической погрешности, то последнюю и принято принимать в качестве основы оценки весовых значений, проводимых измерений. При этом веса результатов измерений принимают обратно пропорциональными квадратам соответствующих им средних квадратических погрешностей.
Так, если обозначить через р и Р веса измерений, имеющие средние квадратические погрешности соответственно m и µ, то можно записать соотношение пропорциональности:

Например, если µ средняя квадратическая погрешность арифметического среднего, а m – соответственно, одного измерения, то, как следует из

можно записать:

т. е. вес арифметического среднего в n раз больше веса единичного измерения.

Аналогичным образом можно установить, что вес углового измерения, выполненного 15-секундным теодолитом, в четыре раза выше веса углового измерения, выполненного 30-секундным прибором.

При практических вычислениях обычно вес одной какой-либо величины принимают за единицу и при этом условии вычисляют веса остальных измерений. Так, в последнем примере если принять вес результата углового измерения 30-секундным теодолитом за р = 1, то весовое значение результата измерения 15-секундным теодолитом составит Р = 4.

Определение размера погрешности

На значение погрешности влияют два параметра:

Это нагляднее можно понять из примера: класс точности прибора составляет 2,5 при диапазоне измерений в пределах 6 МПа. Погрешность прибора вычисляем по формуле пропорций: 6*2,5/100=0,15 МПа. Обозначение на приборе 2,5 означает, что данный прибор при измерении давления может дать погрешность в пределах 2,5% от истинного диапазона. Вычисляются эти данные опытным путём. Замеры давления делаются двумя приборами – образцом и испытуемым манометром. Далее фиксируется разница между показателями. Такая процедура проводится несколько раз для нахождения максимального значения отклонения. Например, диапазон испытуемого барометра 300 бар, а максимальное выявленное отклонение от образца – 3 бар. Процент отклонения высчитывается следующим образом: 3*100/300=1. В итоге определился класс точности прибора – единица.

Погрешности измерений, представление результатов эксперимента

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

№ мензурки	a, мл	b, мл	n	\(\triangle=\frac{b-a}{n+1}\), мл
1	20	40	4	\(\frac{40-20}{4+1}=4\)
2	100	200	4	\(\frac{200-100}{4+1}=20\)
3	15	30	4	\(\frac{30-15}{4+1}=3\)
4	200	400	4	\(\frac{400-200}{4+1}=40\)

Инструментальная точность мензурки равна половине цены деления. Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное. Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

№ мензурки	Объем \(V_0\), мл	Абсолютная погрешность \(\triangle V=\frac{\triangle}{2}\), мл	Относительная погрешность \(\delta_V=\frac{\triangle V}{V_0}\cdot 100\text{%}\)
1	68	2	3,0%
2	280	10	3,6%
3	27	1,5	5,6%
4	480	20	4,2%

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:

Цена деления 4; 20; 3; 40 мл Объем 68; 280; 27; 480 мл Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0\pm 0,1)\ \text{м},\ \ x_2=(4,0\pm 0,03)\ \text{м} $$ Какое из этих измерений точней и почему? Мерой точности является относительная погрешность измерений. Получаем: \begin{gather*} \delta_1=\frac{0,1}{4,0}\cdot 100\text{%}=2,5\text{%}\\ \delta_2=\frac{0,03}{4,0}\cdot 100\text{%}=0,75\text{%} \end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней. Ответ

: \(\delta_2\lt \delta_1\), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч. Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч. Найдите скорость их сближения, абсолютную и относительную погрешность этой величины. Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ \triangle v_1=\frac{10}{2}=5\ (\text{км/ч}),\ \ \triangle v_2=\frac{1}{2}=0,5\ (\text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54\pm 5)\ \text{км/ч},\ \ v_2=(72\pm 0,5)\ \text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20},\ \ v_0=54+72=125\ \text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ \triangle v=\triangle v_1+\triangle v_2,\ \ \triangle v=5+0,5=5,5\ \text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0\pm 5,5)\ \text{км/ч} $$ Относительная погрешность: $$ \delta_v=\frac{5,5}{126,0}\cdot 100\text{%}\approx 4,4\text{%} $$ Ответ:

\(v=(126,0\pm 5,5)\ \text{км/ч},\ \ \delta_v\approx 4,4\text{%}\)

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины. Инструментальная погрешность линейки \(d=\frac{0,1}{2}=0,05\ \text{см}\) Результаты прямых измерений длины и ширины: $$ a=(90,20\pm 0,05)\ \text{см},\ \ b=(60,10\pm 0,05)\ \text{см} $$ Относительные погрешности (не забываем про правила округления): \begin{gather*} \delta_1=\frac{0,05}{90,20}\cdot 100\text{%}\approx 0,0554\text{%}\approx \uparrow 0,056\text{%}\\ \delta_2=\frac{0,05}{60,10}\cdot 100\text{%}\approx 0,0832\text{%}\approx \uparrow 0,084\text{%} \end{gather*} Площадь столешницы: $$ S=ab,\ \ S=90,2\cdot 60,1 = 5421,01\ \text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ \delta_S=\delta_a+\delta_b=0,056\text{%}+0,084\text{%}=0,140\text{%}=0,14\text{%} $$ Абсолютная погрешность: \begin{gather*} \triangle S=S\cdot \delta_S=5421,01\cdot 0,0014=7,59\approx 7,6\ \text{см}^2\\ S=(5421,0\pm 7,6)\ \text{см}^2 \end{gather*} Ответ

: \(S=(5421,0\pm 7,6)\ \text{см}^2,\ \ \delta_S\approx 0,14\text{%}\)